El término
equilibrio implica que un cuerpo ya sea en el plano o en el espacio está en reposo o que su centro de masa se mueve con
velocidad constante. Esta situación es común en
ingeniería y de vital importancia al cuantificar las fuerzas y torques a la cual será sometido un elemento estructural cualquiera. Al analizar un
sistema estático se toma como premisa el hecho de que la aceleración de su centro de masa es cero con respecto a un referencial inercial, asimismo, la aceleración angular alrededor de cualquier eje fijo en este referencial también ha de ser cero.
El
análisis de un cuerpo rígido en condición
estática conlleva la operacionalización de todas las fuerzas involucradas, en tal sentido el presente módulo se cimienta en el
álgebra vectorial tanto en el plano como en el espacio. Por último, debe señalarse que las nociones aquí tratadas serán de gran importancia en subproyectos ulteriores tales como:
mecánica racional,
resistencia de
materiales y todos aquellos estrechamente vinculados con el
diseño de elementos estructurales.
En este material instruccional se introducirá en forma sucinta los lineamientos básicos sobre álgebra vectorial: suma y resta, fundamentalmente. Se presentará los conceptos de
producto vectorial y escalar; los cuales permitirán incorporar lo concerniente al momento de
torsión de una
fuerza. Se desarrollará la
teoría del triángulo de fuerzas, que es una herramienta muy útil, pues permite simplificar en gran medida
problemas que involucren barras o vigas. En determinadas situaciones se hará uso de los
vectores unitarios direccionales como
estrategia de
cálculo; asimismo, se esbozará algunos aspectos básicos del álgebra matricial, dada su relevancia al solventar
sistemas de
ecuaciones. Al final, se ofrecerá una recopilación de algunos problemas que han formado parte de las evaluaciones de cohortes precedentes.
OBJETIVO GENERAL
Al término de éste módulo, el estudiante tendrá la habilidad y pericia necesaria para aplicar los conceptos básicos de estática en la resolución de problemas prácticos que involucren elementos estructurales o mecánicos en equilibrio isostático.
CONTENIDOS
- Operación con vectores: suma, resta y multiplicación.
- Aplicación del Teorema del Seno en la resolución de sistemas estáticos.
- Aplicación del Teorema del Coseno en la resolución de sistemas estáticos.
- Torque de una fuerza.
- Resolución de sistemas estáticos por el método del triángulo de fuerzas.
- Resolución de sistemas estáticos por el método de la descomposición rectangular.
- Resolución de sistemas estáticos por el método geométrico.
- Aplicación de vectores unitarios en la resolución de sistemas estáticos.
CONOCIMIENTOS PREVIOS
- Resolución de sistemas de ecuaciones: cualquier método.
- Trigonometría plana y espacial: relaciones métricas en los triángulos.
- Funciones trigonométricas.
- Perpendicularidad y paralelismo.
- Relaciones, identidades y ecuaciones trigonométricas.
DESARROLLO TEÓRICO
1.1 ¿Qué es un vector y para qué sirven?
Un vector en
física es una cantidad que tiene magnitud,
dirección y sentido al mismo
tiempo. Por ejemplo, una cantidad ordinaria, o escalar, puede ser una distancia de 6 km, una cantidad vectorial sería decir 6 km norte. Los vectores se representan normalmente como segmentos rectilíneos orientados, como
B en la Figura 1; el punto "O" es el origen o punto de aplicación del vector y B su extremo. La longitud del segmento es la medida o módulo de la cantidad vectorial, y su dirección es la misma que la del vector.
Figura 1. Representación gráfica de vectores. Note que el vector
C es la suma de los vectores
A y
B.
El uso sencillo de los vectores así como los cálculos utilizando vectores quedan ilustrados en la Figura 1, que
muestra el
movimiento de una barca para atravesar una corriente de
agua. El vector a, u
A, indica el movimiento de la barca durante un determinado periodo de tiempo si estuviera navegando en aguas tranquilas; el vector b, o
B, representa la deriva o empuje de la corriente durante el mismo periodo de tiempo. El recorrido real de la barca, bajo la influencia de su propia propulsión y de la corriente, se representa con el vector c, u
C. Utilizando vectores, se puede resolver gráficamente cualquier problema relacionado con el movimiento de un objeto bajo la influencia de varias fuerzas.
Este método de resolución de problemas, conocido como adición vectorial, se lleva a cabo según se explica a continuación. Un vector que representa una fuerza se dibuja empezando por el origen "O" en la dirección y con el sentido apropiados. La longitud del vector es proporcional a su
valor real según una
escala determinada, que puede ser un cierto número de centímetros por cada kilómetro. En el
dibujo anterior, la velocidad al remar es de 2,2 km/h, el tiempo transcurrido es 1 hora y la escala es 1 cm por cada km. Por tanto, el vector
A mide 2,2 cm y representa 2,2 km. La velocidad de la corriente del río es de 6 km/h, y se representa con el vector
B que mide 6 cm, lo que indica que la corriente recorre una distancia de 6 km en una hora. Este segundo vector se dibuja con su origen en el extremo del vector
A y en dirección paralela al movimiento de la corriente. El punto
B, extremo del segundo vector, es la posición real de la barca después de una hora de viaje, y la distancia recorrida es la longitud del vector c, u
C (en este caso, unos 6,4 km. El método descrito recibe el nombre de Método Geométrico de Suma de Vectores).
1.2 Magnitudes vectoriales y escalares.
Una magnitud escalar es aquella que solo posee módulo, como por ejemplo: el tiempo, el
volumen, la masa, la
densidad de los cuerpos,
el trabajo mecánico, la cantidad de
dinero entre otras. Las magnitudes escalares se suman o restan a través de los
métodos ordinarios del álgebra; por ejemplo:
2 s + 5 s = 7 s ("s" significa segundo).
A diferencia de las magnitudes escalares, las magnitudes vectoriales poseen dirección y sentido. Por ejemplo:
- El desplazamiento: un avión que vuela una distancia de 160 km hacia el sur.
- La velocidad: un barco que navega a 20 nudos hacia el este.
Una magnitud vectorial se representa por medio de una flecha a una cierta escala. La longitud de la flecha representa el módulo del vector. La línea sobre la que se encuentra es la dirección del vector y el sentido es indicado por la flecha (Figura 2).
Figura 2. Representación gráfica de un vector. La línea punteada es conocida como línea de
acción del vector. Nótese que el vector siempre va acompañado de un "flecha" sobre la letra usada para representarlo.
1.3 Suma y resta de vectores.
Existen dos formas clásicas para realizar dichas
operaciones: una analítica y una gráfica. A continuación se describe en forma sucinta cada una de ellas:
Suma y resta de vectores en forma geométrica
Para sumar más de dos vectores, se emplea la Regla del Polígono, no obstante, si la suma involucra dos vectores se aplica la Regla del Triángulo o la Regla del Paralelogramo.
Regla del Polígono
Consiste en dibujar a una escala adecuada los vectores que se desean adicionar conservando su módulo, dirección y sentido. Uniendo el origen del primero con el extremo del último, obtendrá el vector suma (Figura 3).
Regla del Triángulo
En realidad es un caso particular de la Regla del Polígono, y se aplica a la suma de dos vectores (Figura 4).
Figura 3. En la figura se observa la adición de los vectores
A,
B y
C, por la Regla del Polígono. Es importante señalar que los vectores se representan en negritas o en su defecto con una flechita sobre la letra usada en la grafía.
Figura 4. En la figura se observa la adición de los vectores
A y
B, por la Regla del Triángulo.
Regla del Paralelogramo
Este método se usa cuando los vectores tienen el mismo punto de aplicación (o sea idéntico origen). Se traza una línea punteada paralela a cada vector, el punto de intercepción de dichas líneas se une con el origen y se tendrá el vector resultante (Figura 5).
No se debe olvidar conservar la escala a efecto de cuantificar el módulo del vector resultante, la dirección y sentido se determinan directamente sobre el gráfico. Como puede acusar, los métodos
gráficos requieren de un
juego de escuadras, un transportador y en la medida de las posibilidades una hoja milimetrada. No obstante, la exactitud de los métodos gráficos es sumamente baja, por lo que son inaplicables en la gran mayoría de los cálculos de ingeniería.
Figura 5. En la figura se observa la adición de los vectores
A y
B, por la Regla del Paralelogramo. Detalle como el origen de ambos vectores es el mismo.
Método del paralelogramo (Resta de vectores)
Es análogo a la adición, solo que este caso el sustraendo es un vector opuesto (Figura 6).
Figura 6. Se observan dos vectores
A y
B, si se desea obtener la diferencia entre
A y
B, se dibuja el vector
A y seguido el vector opuesto de
B; la intersección de las paralelas a ambos vectores con el origen común representa el vector diferencia.
Método del triángulo (Resta de vectores)
Es análogo a la adición, no obstante el vector resultante se traza desde la punta del vector sustraendo al vector minuendo (Figura 7).
Figura 7. Dos vectores
A y
B, la diferencia de ambos se obtiene dibujando el vector
A y el vector
B con un origen común, posteriormente se traza el vector resultante desde la punta del vector sustraendo a la punta del vector minuendo.
Suma y resta de vectores en forma analítica
Teorema del coseno
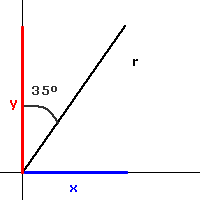
Este teorema es aplicado cuando interactúan dos vectores en el plano (los cuales, en nuestro caso serían fuerzas) y tienen como característica el hecho de presentar un origen común; se requiere conocer los módulos de los vectores, y el ángulo que forman entre si (Figura 8).
- Caso uno. Suma de vectores.

(1)
Donde:
A: módulo del vector A
B: módulo del vector B
A + B: módulo del vector suma A + B
: ángulo en grado encerrado por los vectores
A y
B
Figura 8. Dos vectores
A y
B, ambos se suman por el método del paralelogramo.
- Caso dos. Resta de vectores.

(2)
Donde:
A: módulo del vector A
B: módulo del vector B
A - B: módulo del vector resta A – B
: ángulo en grado encerrado por los vectores
A y
B
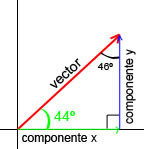
Método de las proyecciones (método de la descomposición rectangular)
Es el más popular en ingeniería. En él se determina la suma de las proyecciones en cada eje para aplicar luego el Teorema de Pitágoras a fin de determinar el módulo del vector suma, y la definición de la
función tangente para la cuantificación del ángulo que forma dicho vector con el eje x positivo.
En general, lo más cómodo es descomponer un vector en sus proyecciones o componentes según dos direcciones ortogonales entre si cuando se trate de problemas en el plano, y en tres, si es en el espacio.
Ejemplo:
Figura 9. En la Figura se observa la coexistencia de los vectores
A,
B y
C. El vector resultante se obtiene a través del Método de las Proyecciones; observe la manera en que se obtienen las proyecciones de cada vector: se descomponen rectangularmente, se halla la resultante en cada eje, se aplica el Teorema de Pitágoras y la función tangente.
Suma sobre el eje x: Ax + Cx – Bx = Sx
Suma sobre el eje y: Ay + By – Cy = Sy
Sx y Sy son las componentes del vector resultante y por ende, ortogonales entre si; tal condición permite aplicar el Teorema de Pitágoras para la determinación del módulo del vector resultante. De igual manera, la definición de la función tangente es usada para el establecer el sentido y la dirección del vector suma.
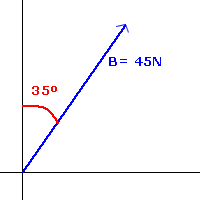
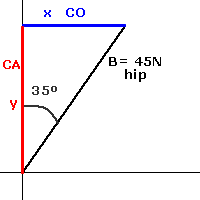
Método del teorema del seno
Este método se aplica en la resolución de sistemas de fuerzas donde coexisten un máximo de tres fuerzas no concurrentes, pero que actúan sobre un mismo cuerpo (Figura 10). Es muy útil al momento de determinar dirección y sentido de un vector, y suele emplearse en conjunción con el teorema del coseno.

(3)
Donde:
A,
B,
C: módulos de los vectores A, B y C.
: ángulo en frente del vector A.
: ángulo en frente del vector B.
: ángulo en frente del vector C.
Figura 10. En la Figura se observa la coexistencia de los vectores
A,
B y
C. Los ángulos internos o cualquiera de los vectores pueden determinarse dado tres
variables.
Suma y resta de vectores en forma analítica en el espacio
Para sumar o restar vectores en el espacio se debe conocer previamente las componentes de los vectores a lo largo de cada eje (Figura 11), seguido, se adiciona o restan las proyecciones; obteniéndose las componentes ortogonales del vector resultante.
Ejemplo:
Sea los vectores:
A = axi + ayj + azk (4)
B = bxi + byj + bzk (5)
Su suma se establece como:
A +
B = (ax + bx)i + (ay + by)j + (az + bz)k (6)
La diferencia de ambos esta dada por:
A –
B = (ax - bx)i + (ay - by)j + (az - bz)k (7)
Las letras i, j y k reciben el nombre de vectores unitarios de dirección, pues son vectores cuya módulo vale uno, pero que poseen dirección y sentido. La letra i se asocia al eje x positivo, la letra j se asocia al eje y positivo y por último, la letra k se asocia al eje z positivo.
El vector unitario de un vector cualquiera puede obtenerse a través de la siguiente expresión:

(8)
O sea, se divide las componentes ortogonales del vector entre su módulo (algunos
libros llaman al módulo, magnitud del vector). Si se suman los cuadrados de las componentes ortogonales de un vector unitario dará la unidad (uno). En términos generales cualquier vector se puede representar de la forma siguiente:

(9)
Donde:
ax: componente del vector a lo largo del eje x.
ay: componente del vector a lo largo del eje y.
az: componente del vector a lo largo del eje z.
Figura 11. En la Figura se observa un vector en el espacio. Los vectores ax, ay y az se conocen como componentes ortogonales del vector.
1.4 Multiplicación de vectores: producto escalar y producto vectorial.
Producto escalar
Es una cantidad escalar igual al producto de las magnitudes de dos vectores y el coseno del ángulo encerrados por ellos (Figura 12).
Algebraicamente, el producto vectorial esta dado por:

(10)
Algunas propiedades del producto vectorial son:
- Propiedad conmutativa: A.B = B.A(11)
- Propiedad distributiva: A.(B + C) = A.B + A.C (12)
Figura 12. El producto escalar de dos vectores se obtiene multiplicando sus magnitudes por el coseno del ángulo .
Si se conoce las componentes de los vectores:
A = Axi + Ayj + Azk (13)
B = Bxi + Byj + Bzk (14)
Nos queda...
C =
A.
B = Ax.Bx + Ay.By + Az.Bz(15)
Producto vectorial
Si tenemos dos vectores coplanares (que se encuentra en el mismo plano)
A y
B, el producto vectorial generará un vector
C ortogonal al plano conformado por
A y
B, cuya magnitud esta dada por:

(16)
El sentido del vector
C está determinado por el avance de un tornillo de cuerda derecha cuando se gira de A hacia B, a través del ángulo . Una regla más conveniente puede usarse para determinar la dirección de
C, es la Regla de la Mano Derecha. Los cuatro dedos de la mano derecha apuntan a lo largo de
A y luego se enrollan hacia
B a través del ángulo . La dirección del pulgar derecho erecto es la dirección de
C (Figura 13).
Figura 13. El producto vectorial de los vectores
A y
B genera un nuevo vector
C ortogonal a los dos primeros.
Las propiedades del producto escalar son:
A x
B = - (
B x
A) (17)
Si
A es paralelo a
B;
A x
B = 0 (18)
Si
A es perpendicular a
B;
A x
B =
A.
B(19)
Ley distributiva;
A x (
B x
C) =
A x
B +
A x
C(20)
Cuando se conoce las componentes de los vectores, se usa la siguiente expresión:

(21)
En
matemática la expresión antes mostrada se deriva del "Teorema del Cofactor".
1.5 Generalidades sobre fuerza.
Fuerza, en física, es cualquier acción o influencia que modifica
el estado de reposo o de movimiento de un objeto. La fuerza que actúa sobre un objeto de masa
m es igual a la variación del momento lineal (o cantidad de movimiento) de dicho objeto respecto del tiempo. En el Sistema Internacional de unidades, la fuerza se mide en newtons: 1
newton (N) es la fuerza que proporciona a un objeto de 1 kg de masa una aceleración de 1 m/s2.
La fuerza es una magnitud vectorial, puesto que el momento lineal lo es, y esto significa que tiene módulo, dirección y sentido. Al conjunto de fuerzas que actúan sobre un cuerpo se le llama sistema de fuerzas. Si las fuerzas tienen el mismo punto de aplicación se habla de fuerzas concurrentes. Si son paralelas y tienen distinto punto de aplicación se habla de fuerzas paralelas.
Cuando sobre un objeto actúan varias fuerzas, éstas se suman vectorialmente para dar lugar a una fuerza total o resultante. Si la fuerza resultante es nula, el objeto no se acelerará: seguirá parado o detenido o continuará moviéndose con velocidad constante. Esto quiere decir que todo cuerpo permanece en
estado de reposo o de movimiento rectilíneo y uniforme mientras no actúe sobre él una fuerza resultante no nula (equilibrio de traslación).
Una fuerza es siempre una acción mutua que se ejerce entre dos objetos (fuerzas exteriores) o entre dos partes de un mismo objeto (fuerzas interiores). Así, un objeto experimenta una fuerza cuando otro objeto lo empuja o tira de él. Si una bola de billar golpea a otra que está en reposo y ambas se mueven después de chocar es porque existen fuerzas que actúan sobre cada una de las bolas, ya que las dos modifican sus movimientos. Por sí mismo, un objeto no puede experimentar ni ejercer ninguna fuerza.
Las fuerzas aparecen siempre entre los objetos en pares de acción y reacción iguales y opuestas, pero que nunca se pueden equilibrar entre sí puesto que actúan sobre objetos diferentes.
Esta acción mutua no siempre se ejerce entre dos objetos en contacto. En muchas ocasiones parece tener lugar "a distancia"; éste es el caso de un objeto atraído por
la Tierra, y viceversa, con una fuerza que es el peso del objeto. Entonces se habla de campos de fuerzas, y en el caso
concreto del objeto atraído por la
Tierra se habla del campo gravitatorio terrestre; las cargas eléctricas se atraen o se repelen debido a la presencia de un campo eléctrico.
1.6 Momento de torsión de una fuerza.
El momento, en física, es una medida del efecto de rotación causado por una fuerza. Es igual a la magnitud de la fuerza multiplicada por la distancia al eje de rotación, medida perpendicularmente a la dirección de la fuerza. En vez de describir la
dinámica de rotación en función de los momentos de las fuerzas, se puede hacer en función de pares de fuerzas.
Un par de fuerzas es un conjunto de dos fuerzas iguales y de sentido contrario aplicadas en puntos distintos. El momento del par de fuerzas o torque se representa por un vector perpendicular al plano del par, cuyo módulo es igual al producto de la intensidad común de las fuerzas por la distancia entre sus rectas soporte, y cuyo sentido está ligado al sentido de rotación del par por la "regla del sacacorchos o regla de la mano derecha".
En forma simple, el momento de una fuerza viene a ser el producto vectorial del
radio vector de la fuerza por el vector de la fuerza generadora del momento (Figura 14).

(22)
Donde:
: momento asociado al vector fuerza, N.m
r: radio vector, m
F: vector fuerza, N
También puede expresarse como:

(23)
Figura 14. Una fuerza
F actúa en un punto A de un cuerpo, ello hace que éste rote alrededor del punto "o", el cual recibe el nombre de centro instantáneo de rotación. La distancia más pequeña que existe entre "o" y la línea de acción del vector fuerza recibe el nombre de "brazo del vector fuerza";
r es conocido como radio vector de la fuerza, y es un vector cuyo origen se encuentra en "o" y extremo en el punto de aplicación de la fuerza.
1.7 Condiciones de equilibrio estático en un sistema mecánico.
El equilibrio de un sólido sometido a la acción de un sistema de fuerzas coplanarias (que pertenecen al mismo plano) no paralelas se puede reducir al estudio de dos sistemas de fuerzas paralelas, sin más que tener en cuenta las componentes horizontales y verticales por separadas. Las dos condiciones de equilibrio se expresan a continuación;
- Equilibrio de traslación: la resultante o suma vectorial de todas las fuerzas aplicadas al cuerpo debe ser cero. Esto equivale a decir que la suma algebraica de las fuerzas o de sus componentes aplicadas a un cuerpo en una dirección cualquiera debe ser cero. Si se hace el análisis del sistema en función de un sistema referencial ortogonal entre si, ello equivale a:

(24)
La fuerza resultante a lo largo del eje x debe ser cero.

(25)
La fuerza resultante a lo largo del eje y debe ser cero.

(26)
La fuerza resultante a lo largo del eje z debe ser cero.
- Equilibrio rotacional: la suma algebraica de los momentos de torsión de todas las fuerzas, con respecto a un eje cualquiera perpendicular al plano de las mismas debe ser cero. Si se hace el análisis del sistema en función de un sistema referencial ortogonal entre si, ello equivale a:

(27)
La sumatoria de los momentos alrededor del eje x debe ser cero.

(28)
La sumatoria de los momentos alrededor del eje y debe ser cero.

(29)
La sumatoria de los momentos alrededor del eje z debe ser cero.
1.8 Reacciones en puntos de apoyos.
Como se mencionó en el apartado 1.5 una fuerza es siempre una acción mutua que se ejerce entre dos objetos (fuerzas exteriores) o entre dos partes de un mismo objeto (fuerzas interiores). En tal sentido, al momento de estudiar sistemas estáticos debe tenerse especial cuidado al ubicar las reacciones sobre los apoyos (vigas simplemente apoyadas,
articulaciones o sus equivalentes). En términos generales, si la superficie es perfectamente lisa la reacción se dibuja perpendicular al punto de apoyo; en caso contrario, el apoyo poseerá una reacción con dos componentes: una reacción vertical y otra horizontal, cuya suma vectorial genera la reacción total equivalente (Figura 15).
Figura 15. En una barra simplemente apoyada en dos elementos perfectamente lisos coexisten dos reacciones ortogonales a la superficie de contacto (arriba). Una articulación o bisagra posee generalmente dos reacciones: una vertical y otra horizontal, las cuales equilibran el sistema.
Al estudiar sistemas estáticos en el espacio, solo debe incluirse una componente adicional en la reacción (a lo largo del eje z).
El hecho de obtener reacciones negativas al determinar las fuerzas incógnitas de un sistema estático, conlleva a concluir que las reacciones poseen sentido opuestos al asignado; este principio se extrapola a cualquier fuerza con valor negativo (tensión, por ejemplo).
Se advierte que a nivel de los apoyos, además de las reacciones señaladas, se generan momentos o torques equilibrantes; no obstante, esta situación se aborda con mayor profundidad en
mecánica racional y/o resistencia de materiales. Asimismo, a lo largo de este módulo se ignora las deformaciones mecánicas que experimentan las barras o cables tensores como consecuencia de las fuerzas de compresión o tracción actuantes.
1.9 Metodología para resolver sistemas isostáticos.
- Elabore un dibujo del objeto considerado
- Dibuje un diagrama de cuerpo libre y asigne una letra a todas las fuerzas externas que actúen sobre el objeto. Intente adivinar la dirección correcta de cada fuerza. Si usted elige una dirección que conduce a un signo negativo en su solución para una fuerza, no se alarme; esto simplemente se significa que la dirección de la fuerza es opuesta a la que usted eligió.
- Descomponga todas las fuerzas en componentes rectangulares, pero elija un sistema de coordenadas conveniente. Aplique después la primera condición de equilibrio. Recuerde conservar los signos de las diferentes componentes de fuerza.
- Elija un eje conveniente para calcular el momento de torsión neto sobre el objeto. Recuerde que la elección del origen para la ecuación de momento de torsión es arbitraria; por lo tanto, elija un origen que simplifique sus cálculos lo más posible. Volverse un adepto de lo anterior es muy práctico.
- La primera y la segunda condiciones de equilibrio brindan un conjunto de ecuaciones lineales con varias incógnitas. Todo lo que resta es resolver las ecuaciones simultáneas respectos de las incógnitas en función de las cantidades desconocidas.
PROBLEMAS PROPUESTOS CON RESPUESTAS
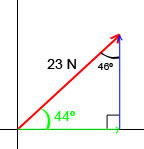
- Calcular para la fuerza de la figura adjunta, tomando 1 cm = 5 N. Hallar gráficamente la componente horizontal y vertical; verificar analíticamente. Sol. a) 25,7 N y 30,6 N
- Un bloque se arrastra hacia arriba por un plano inclinado 20° sobre la horizontal con una fuerza F que forma un ángulo de 30° con el plano. Determinar: El valor de F para que su componente Fx paralela al plano sea de 16 N. El valor de la componente Fy perpendicular al plano. Sol. a) 18,5 N b) 9,2 N
- Utilizando el método de descomposición rectangular, hallar la resultante y el ángulo que forma con la dirección positiva del eje x, de las siguientes fuerzas:
- 200 N en el eje x dirigida hacia la derecha.
- 300 N, 60° por encima del eje x, hacia la derecha.
- 100 N, 45° sobre el eje x, hacia la derecha.
- 200 N en la dirección negativa del eje y. Sol. 440,49 N y 17,23 °.
- Dos fuerzas F1 y F2 actúan sobre un punto, F1 es de 8 N y su dirección forma un ángulo de 60° por encima del eje x en el primer cuadrante, F2 es de 5 N y su dirección forma un ángulo de 53° por debajo del eje x en el cuarto cuadrante, determinar:
- Las componentes de la resultante. Sol. 7,01 N y 2,93 N.
- La magnitud de la resultante. Sol. 7,6 N.
- La magnitud de la diferencia F1 – F2 Sol. 11 N.
- Dos hombres y un muchacho quieren empujar un bloque en la dirección x de la figura, los hombres empujan con las fuerzas F1 y F2.
- ¿Qué fuerza mínima deberá emplear el muchacho para lograr el cometido?. Sol. 46,6 N
- ¿Qué dirección tendrá dicha fuerza?. Sol. perpendicular a x.
- Dos pesos de 10 N están suspendidos en los extremos de una cuerda que pasa por una polea ligera sin rozamiento. La polea está sujeta a una cadena que cuelga del techo. Determinar:
- La tensión de la cuerda. Sol. 10 N.
- La tensión de la cadena. Sol. 20 N
- Para hallar el peso y el centro de gravedad de una barra gruesa de 1,6 m de longitud, dos hombres, A y B, de 60 y 80 Kgf respectivamente, realizan la siguiente experiencia. Apoyan la barra por uno de sus puntos intermedios y permaneciendo B sobre uno de los extremos de la barra se mantiene horizontal (en equilibrio), estando el apoyo situado a 0,75 m de él. Después se coloca A sobre el mismo extremo y para que la barra continúe horizontal (en equilibrio) el apoyo tiene que estar a 0,80 m de él. Dibujar los diagramas correspondientes y calcular: a) el peso de la barra y b) la posición de su centro de gravedad. Sol. a) 240 Kgf, b) 1 m del extremo en el que se colocan los hombres.
- El extremo superior de una barra uniforme de 2 m de longitud y 80 N de peso está articulado a un soporte, mientras que el inferior se halla unido a una cuerda horizontal que mantiene la barra formando un ángulo de 40º con la vertical. Calcúlese la tensión en la cuerda. Sol. Sol. 33,55 N.
- Un bastón homogéneo de masa m y longitud l se coloca en el interior de un hemisferio perfectamente liso de radio r. Hallar la posición de equilibrio del bastón. Sol.
 ;
;  ;
;  (ángulo de equilibrio)
(ángulo de equilibrio)
- Para sacar un automóvil de una zanja, se ata al extremo A de una cuerda AOB a un árbol y el otro extremo B al coche. En el punto medio O de la cuerda AB se ejerce un empuje de 100 Kp en dirección perpendicular a AB. Calcular la tensión T en la cuerda sabiendo que el ángulo AOB es de 170º. Sol. 573 Kp.
- Una barra uniforme AB, de 4 m de longitud y 50 Kgf de peso está unida a un mástil por medio de una articulación en A y el otro extremo B, unido al mástil por medio de una cuerda, en dicho punto pende una carga de 200 Kgf. La barra y la cuerda forman con el mástil ángulos de 60º y 70º, respectivamente. Calcular la tensión de la cuerda y la reacción RA en el extremo inferior de la barra. Sol. Tensión: 254,5 Kgf; Reacción en A: 289 Kgf con dirección 34º, referido al eje x positivo.
- Una fuerza F = 600i – 300j + 400k actúa en el punto x = 2, y = - 4, z = - 8. Determina el torque generado por dicha fuerza. Sol. 7113,4 N.m
- En el extremo inferior de una escalera se apoya contra una pared vertical y sobre un suelo horizontal. El extremo superior está unido a la pared por medio de una cuerda horizontal de 9 m de longitud. La escalera tiene una longitud de 15 m, pesa 50 N y su centro de gravedad se halla situado a 6 m de su extremo inferior. Determinar la tensión en la cuerda cuando un hombre de 75 N de peso se encuentra a una distancia de 3 m del extremo superior. Sol. 60 N.
- Dado un plano inclinado sin rozamiento que forma un ángulo de 32º con la horizontal y un bloque prismático de 200 lbf de peso apoyado en él, calcular la fuerza mínima que es necesaria aplicar al bloque para que ascienda sobre dicho plano. Sol. 200 x Sen 32º lbf.
- Determinar en que punto de una barra de peso despreciable, se debe colocar un cuerpo de manera que el peso soportado por un muchacho en uno de sus extremos sea la tercera parte del que soporta un hombre en el otro. Sol. ¾ de la longitud de la barra.
- Una escalera AB de 5 m de longitud y 30 Kgf de peso tiene el centro de gravedad a 5/3 m de su extremo inferior. Se apoya con el extremo A en un suelo rugoso y el B contra una pared vertical pulida en un punto situado a 4 m del suelo. Hallar las reacciones de la pared y del suelo Sol. Reacción de la pared: 7,5 Kgf; Reacción del suelo: 31 Kgf con dirección 76º positivo referido al suelo.
- Una barra uniforme AB de 1 m de longitud y 20 Kp de peso está unida a un mástil por medio de una articulación en su extremo A y del otro extremo B pende una carga de 200 Kp. Hallar la fuerza necesaria para soportar la barra en un punto C situado a 0,30 m de la articulación por medio de una cuerda que forma 34º con el mástil. Sol. 844,39 Kp
- Los extremos de una cuerda de 11 m de longitud se unen a dos grandes ganchos colocados en un techo horizontal y separado entre sí 9 m. A los 4 m de uno de los extremos de la cuerda se une un peso de 100 lbf. Calcular la tensión en los dos segmentos de la cuerda. Sol. 70 lbf y 95 lbf.
- En la figura se representa el esquema de una grúa soportando un peso de 900 Kp. El mástil AC tiene una longitud de 3 m y la barra AB tiene 5 m de longitud, con una articulación A, y es mantenida por el cable CB. Suponiendo que el peso de AB es despreciable, calcular la tensión T en el cable y la fuerza de compresión P en AB.. Sol. T = 1.038 Kp. ; P = 1.500 Kp. Sol: 833 Kp hacia abajo, aplicada a 2,28 m del apoyo izquierdo
- Hallar la resultante de las cuatro fuerzas indicadas en el siguiente diagrama mostrado a continuación.
- Un cilindro de peso w y radio R se va a levantar en un escalón de altura h, como se muestra en la figura. Se enrolla una cuerda alrededor del cilindro y se jala horizontalmente. Suponiendo que el cilindro no desliza sobre el escalón, encuentre la fuerza mínima F necesaria para el cilindro y la fuerza de reacción en P ejercida por el escalón sobre el cilindro. Sol.

- La figura muestra una fuerza vertical aplicada tangencialmente a un cilindro de peso uniforme w. El coeficiente de fricción estática entre el cilindro y todas las superficies es de 0,50. Encuentre, en función de w, la máxima fuerza F que puede aplicarse sin ocasionar que gire el cilindro. (Sugerencia: cuando el cilindro este a punto de deslizar, ambas fuerzas de fricción están en sus valores máximos. ¿Por qué?) Sol.

- Según el caso de la figura adjunta determinar el peso del cuerpo suspendido si la tensión de la cuerda diagonal es de 20 N. Sol. 14,1 N.
- Hay que bajar una caja fuerte de 2.000 N a velocidad constante por una de 4 m de longitud, desde un camión de 2 m de altura. El coeficiente de rozamiento entre la caja fuerte y la rampa es de 0,30. Determinar:
- ¿Hay que empujar o frenar la caja?. Sol: Frenar
- ¿Qué fuerza paralela a la rampa es necesaria?. Sol: 480 N
- Una barra uniforme de peso w y longitud L se sostiene en sus extremos por medio de una piscina sin fricción, como se muestra en la figura adjunta. Determine el valor de equilibrio del ángulo . Sol. 60 º.
- Dos barras uniformes de igual peso W e igual longitud (AC = BC = 2L) están articuladas en C y se apoyan simétricamente en D y E sobre dos vástagos transversales perfectamente lisos. Se da el segmento DE = 2a. Determine el ángulo de equilibrio, la presión contra los vástagos y la reacción de la articulación. Sol.
 ;
;  ;
; 
- Una esfera de peso W se sostiene mediante una cuerda AB y presiona una pared vertical lisa AC. Si es el ángulo entre la cuerda y la pared, determinar la tensión la tensión en la cuerda y la reacción de la pared sobre la esfera. Sol. :
 ;
; 
- La figura adjunta muestra a un chango de 10 kg que sube por una escalera uniforme de 120 N y longitud L. Los extremos superior e inferior de la escalera descansan sobre superficies sin fricción. El extremo inferior está fijado a la pared mediante una cuerda horizontal que puede soportar una tensión máxima de 110 N. Encuentre la distancia máxima d que el chango puede subir por la escalera antes de que se rompa la cuerda. Exprese su respuesta como una fracción de L. Sol. 0,876 L
- La figura adjunta muestra una grúa de 3000 kg de masa que soporta una carga de 10.000 kg. La grúa se articula con un pasador liso en A y descansa contra un soporte liso en B. Encuentre las fuerzas de reacción en A y B. Sol. RA = 66.000 Kgf ; RB = 13.000 Kgf.
- Un tiburón de 10.000 N está sostenido por medio de un cable unido a una barra de 4,00 m que está articulada en la base. Calcule la tensión necesaria para mantener el sistema en la posición mostrada en la figura adjunta. Encuentre las fuerzas horizontal y vertical ejercidas sobre la base de la barra. (Ignore el peso de la barra.). Sol. T = 5076,14 N ; RAX = 4.770 N ; RAY = 8.263,85 N
- La figura anexa muestra una armadura que soporta una fuerza hacia abajo de 1.000 N aplicada al punto B. Ignore el peso de la armadura y aplique las condiciones de equilibrio para demostrar que nA = 366 N y nB = 634 N
- La viga AB es uniforme y tiene una masa de 100 kg. Descansa en sus extremos A y B y soporta las masas como se indica en la figura anexa. Calcular la reacción en los soportes? Sol. RA = 183,3 Kgf ; RB = 116,7 Kgf.
- Determinar la tensión sobre la cuerda AC (Fig. anexa) si M pesa 40 Kgf. Sol. 51,42 Kgf.
- Encontrar la magnitud y la posición de la fuerza resultante del sistema de fuerzas presentado en la figura. Las coordenadas se dan en pies. Sol. 22,23 lbf, la línea de acción es 9,14 = 20,06x + 9,57y
- La estructura mostrada sostendrá una carga de 6000 N (bloque del centro). Suponiendo que la máxima fuerza de tracción que puede soportar la barra AB es de 3500 N, determine si la estructura cederá. Sol. Si, la estructura cederá.
- Encontrar la tensión a la cual están sometidos los cables señalados en la figura. Sol. 221,047 N; 98,856 N
- Determine el valor del ángulo alfa para que el sistema se encuentre en equilibrio; asimismo, calcule el valor de la tensión BA y BC. Sol. Considerando que ambas tensiones son iguales, 35,015 º
- Dos fuerzas paralelas, del mismo sentido, tienen magnitudes de 20 N y 30 N. La distancia de la línea de acción de la resultante a la fuerza mayor es de 0,8 m. Encontrar la distancia entre las fuerzas. Sol. 2 m
- Encontrar la magnitud, dirección y sentido de la fuerza F, de tal manera que el sistema permanezca estático. Sol. 799,52 N y 145,86 º medidos desde el eje x positivo.
- Determine el valor de la fuerza F, para que el sistema permanezca en equilibrio. La fuerza F es paralela al plano, P tiene un peso de 150 N y Q pesa 3050 N. No existe fricción entre el cuerpo Q y el plano. Sol. 1835,4 N
- Dos fuerzas paralelas, del mismo sentido, están separadas por una distancia de 0,2 m. Si una de las fuerzas es de 13 N y la línea de acción de la resultante está a 0,08 m de la otra. Encontrar: la magnitud de la resultante, y la magnitud de la otra fuerza. Sol. 6,5 N y 19,5 N respectivamente.
- Una bola de acero de 6875 N está suspendida por medio de tres cuerdas: A, B y C. Las coordenadas de A son: x = - 4, y = 6, z = 0; Las coordenadas de B son: x = - 8, y = -5, z = 1; Las coordenadas de C son: x = 4, y = -4, z = 0. Las tres cuerdas coinciden en un punto ubicado dentro de la bola con coordenadas: x = 0, y = 0, z = -10. Calcula las tensiones de cada cuerda. Sol. TA = 3420,69 N; TB = 653,39 N; TC = 4154,25 N
- Determine la tensión del cable AB. El peso de la barra CD es 2500 N, su longitud 3,50 m. La barra posee un peso uniformemente distribuido. Sol. 11353,85 N
- Dadas las tres fuerzas siguientes: F1 = 500i ;F2 = 0i – 200j + 100k ; F3 = -100i + 50j – 400k. Determina el torque resultante de las fuerzas anteriormente presentadas, con respecto al origen O, si se aplican al punto: x = 4, y = -3, z = 15. Utilizar la fuerza resultante para determinar el torque resultante. Sol. 3150i + 10200j + 1200k
- Calcular el peso P necesario para mantener el equilibrio en el sistema mostrado en la Fig. anexa, en la cual A pesa 100 kgf y Q 10 kgf. El plano y las poleas son lisas. La cuerda AC es horizontal y la cuerda AB es paralela al plano. Calcúlese también la reacción del plano sobre el peso A. Sol. P = 30 Kgf ; N = 80,83 Kgf.

- ¿Puede estar un cuerpo en equilibrio cuando sobre él actúa una fuerza?
- Un globo se mantiene en el aire sin ascender ni descender. ¿Está en equilibrio?, ¿qué fuerzas actúan sobre él?
- Si se tira de los extremos de una cuerda en equilibrio con dos fuerzas iguales y de dirección opuesta, ¿por qué la tensión total en la cuerda es cero?
- Un caballo está enganchado a un carro. Cómo el carro tira del caballo hacia atrás con la misma fuerza que éste tira del carro, ¿por qué no permanece el carro en equilibrio, independientemente de lo que tire el caballo?
- ¿Cómo se puede empujar hacia abajo el pedal de una bicicleta y lograr que la bicicleta se mueva hacia adelante?
- Para empujar una caja hacia arriba por una rampa, ¿es mejor empujarla horizontal o paralelamente a la rampa?
- ¿De qué depende el coeficiente de rozamiento entre dos superficies?
- ¿Puede el coeficiente de rozamiento ser mayor que la unidad?. En caso afirmativo dé un ejemplo; de lo contrario explique por qué no puede serlo.
PROBLEMAS PROPUESTOS SIN RESPUESTAS
- Una esfera sólida de radio R y masa M se coloca en una cuña, como se ilustra en la figura. Las superficies interiores de la cuña no ofrecen fricción. Determine las fuerzas ejercidas por la cuña sobre la esfera en los dos puntos de contacto. a) La tensión en la barra horizontal que conecta las dos patas de la escalera,
b) Las fuerzas normales en A y B, y
c) Las componentes de la fuerza de reacción en la articulación C que la pata izquierda de la escalera ejerce sobre la pata derecha.
(Sugerencia: Trate cada pata de la escalera por separado.)
- Una escalera de tijera de peso despreciable se construye como se muestra en la figura adjunta. Una pintora de 70,0 kg de masa está parada sobre la escalera a 3,00 m del punto inferior. Suponga al piso sin fricción y encuentre, a) La tensión en el cable y
b) Las componentes de la fuerza de reacción ejercida por la pared sobre la viga en términos de w, d, L y .
- Un letrero uniforme de peso w y ancho 2L cuelga de una ligera viga horizontal, articulada en la pared y soportada por un cable (Fig. anexa). Determine
- Una torre de transmisión se sostiene de tres cables los cuales están anclados mediante pernos en B, C y D. Si la tensión en el alambre AD es de 650 lbf, determine las componentes de la fuerza ejercida por el alambre sobre el perno en D.
- Una barra uniforme AB, de 4 m de longitud y 150 Kgf de peso está unida a un mástil por medio de una articulación en A y el otro extremo B, unido al mástil por medio de una cuerda, en dicho punto pende una carga de 850 Kgf. La barra y la cuerda forman con el mástil ángulos de 40º y 60º, respectivamente. Calcúlese la tensión de la cuerda y la reacción RA en el extremo inferior de la barra.
- Determinar en que punto de una barra de peso despreciable, se debe colocar un cuerpo de manera que el peso soportado por un muchacho en uno de sus extremos sea la quinta parte de la que soporta un hombre en el otro.
- Determínese la magnitud de las fuerzas P y Q, sabiéndose que la de la fuerza resultante sobre el gancho es de 500 N, con dirección 14º medidos a partir de la horizontal en sentido anti-horario.
- Determine las tensiones de los cables, sabiendo que la fuerza ascensional del globo es de 2.895 lbf
- Un oso hambriento que pesa 700 N camina sobre una viga con la intención de llegar a una canasta de comida que cuelga en el extremo de la viga. Ésta es uniforme, pesa 200 N y su largo es igual a 6 m; la canasta pesa 80 N. Si el alambre puede soportar una tensión máxima de 900 N, ¿cuál es la distancia máxima que el oso puede caminar antes de que se rompa el alambre?
 y gráficamente se representan como una flecha en un sistema de coordenadas.
y gráficamente se representan como una flecha en un sistema de coordenadas. 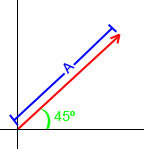


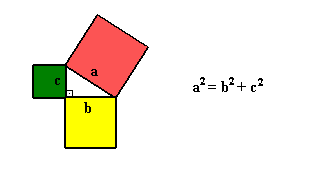
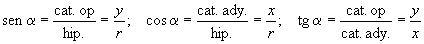
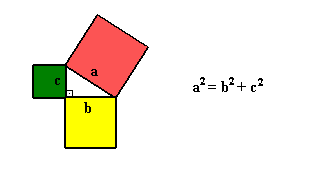
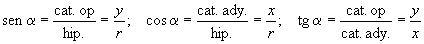

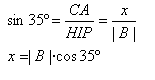
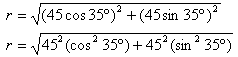








 (1)
(1)
 (2)
(2)
 (3)
(3)
 (8)
(8) (9)
(9)
 (10)
(10)
 (16)
(16)
 (21)
(21) (22)
(22) (23)
(23)
 (24)
(24) (25)
(25) (26)
(26) (27)
(27) (28)
(28) (29)
(29)


 ;
;  ;
;  (ángulo de equilibrio)
(ángulo de equilibrio) 








 ;
;  ;
; 

 ;
; 





















