INTRODUCCION

egún el texto se representan como : y gráficamente se representan como una flecha en un sistema de coordenadas.

La magnitud del vector es la longitud de la flecha y se representa con la misma letra del vector pero sin negrita. La direcci ón se indica escribiendo los grados de inclinación que tiene un vector con repecto a uno de los ejes, en el caso de este ejemplo se indica que el Vector A tiene una inclinación de 45 grados con respecto al eje x.
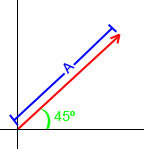
Para efectos prácticos, un vector se compone en realidad de varios sub-vectores que están pegados a alguno de los ejes de coordenadas, es decir, que su línea de acción está justo sobre alguno de los ejes. A estos sub-vectores se les llama en realidad Componentes Vectoriales o Componentes Rectangulares. Se les llama componentes recangulares por que forman porque tienen ángulos rectos entre ellos.

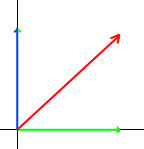El vector está en rojo. Su compomente x en verde, y su componente y en azúl. El componente x y y juntos son los componentes rectangulares del vector. se obtiene el mismo resultado en un punto si se le aplica un vector, que si se le aplican todos los componentes de el mismo vector.

Uno puede encontrar los componentes de un vector se puede hacer trazando una línea desde la punta de la flecha hasta el eje coordenado del que se quiera obtener el componente. Pero es poco práctico y poco exacto es mejor usar el método analítico para obtener los componentes de un Vector. para lograrlo se necesita utilizar algunas herramientas que el buen pitágoras nos dejó, así como algunas herramientas de la geometría. Para poder usar la geometría tenemos que pensar en el vector como un triángulo rectángulo. La longitud de la hipotenusa de ese triángulo es la longitud del Vector, y cada uno de los catetos del triángulo son los componentes rectángulares del vector.

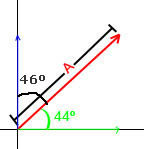
Se puede pensar en el vetor (de dos dimensiones) como un triángulo. la hipotenusa es el vector. y sus catetos (en verde y azúl) serían las componentes x y y del vector. Ya que se tiene un triángulo representando el vector, se pueden utilizar las herramientas de la geometría para obtener los componentes rectangulares. Los ángulos internos de este triángulo son las son las direcciones de los vectores. y podemos obtener los tres ángulos internos con un proceso muy simple: Nos dieron un vector a 44º con respecto al eje x. El primer ángulo interno es de 44º. En un triángulo rectangulo el ángulo entre los catetos es de 90º. Y por último, sabemos que la suma de los tres ángulos internos de un triángulo siempre va a ser igual a 180º. Así que podemos obtener el valor del tercer ángulo así 180º-(44º+90º) = 46º. Y así ya tenemos los tres ángulos internos de el triángulo.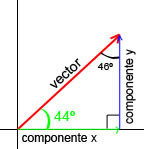

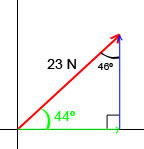Para obtener las magnitudes de los componentes rectangulares, se traza un triángulo cuya hipotenusa va a tener la misma longitud e inclinación que el vector original. en este caso el vector A tiene una magnitud de 23 newtons. Se traza un cateto paralelo al eje x desde el inicio del vector hasta el extremo final. Y se traza el otro cateto paralelo al eje y desde el final del primer cateto, hasta el final de la hipotenusa. Ya teniendo un triángulo se puede utilizar cualquier método geométrico para encontrar la longitud de los lados. Y como la longitud de los lados es igual a la magnitud de los vectores. Al encontrar la longitud de los lados se obtiene la magnitud del vectores y de sus componentes rectangulares. En realidad se podría utilizar cualquier método de resolución de triángulos para hallar la magnitud de los componentes rectangulares, pero como un vector con sus componentes siempre van a formar triángulos rectos se usa el teorema de pitágoras y las definiciones de las funciones trigonométricas en un método llamado descomposición rectangular de vectores

descomposición rectangular de vectores

	En geometría se usan letras para referirse a los lados y ángulos de un triángulo. Se usan las letras mayúsculas A y B para representar los lados de un triángulo rectángulo; y C para representar su hipotenusa. A veces tambien se usa HIP para referirse a la hipotenusa de un triángulo. Y se usan las letras minúsculas a, b, y c para referirse al ángulo que se encuentra justo enfrente del lado correspondiente A, B, y C. Ésta relación se debe a que si hacemos que el ángulo a sea más grande, estamos haciendo que el lado A sea más grande tambien. así: si a crece A (el cateto opuesto a a)tambien crece si b crece B (el cateto opuesto a b)tambien crece si c crece C tambien crece. Pero como esto es un vector. c siempre va a ser de 90º
	Y es así como los lados y los ángulos de un triángulo están relacionados. Ya seriamente, a cualquier lado que no sea la hipotenusa se le llama cateto. Al cateto que está justo enfrente del ángulo que estemos usando será el cateto opuesto al ángulo. El cateto que este al lado del ángulo será el cateto adyacente al ángulo al que se está utilizando como referencia . Ya que uno maneja bien está ecléctica nomenclatura pues podemos pasar a la parte jugosa de ésto que es hallar los componentesrectángulares de un vector.

Y ese choro es en realidad una forma muy poco ortodoxa de explicar el porqué de las funciones trigonométricas. Diciendo lo mismo, pero más propiamente diríamos:

• A, el cateto puesto a a, está en función de a y de la hipotenusa.
• B, el cateto opuesto a b, está en función de b y de la hipotenusa.

Lo anterior no es estríctamente verdadero pero nos pone muy cerca ya de poder descomponer un vector en sus componentes rectangulares usando la los catetos de un triángulo rectángulo. para lograrlo nos valdremos de:

El dichoso teorema de pitágoras:

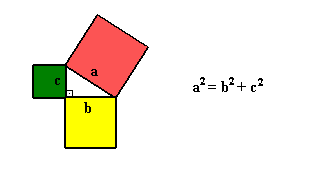
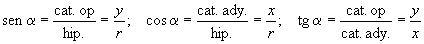
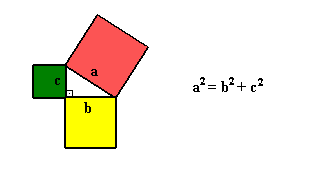
Las funciones trigonométricas básicas:

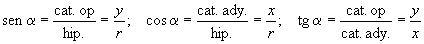
para nuestra incumbencia:
cat. op.= CO = Cateto opuesto.
cat. ady. = CA = Cateto adyacente.
x= compomente rectangular en x del vector.
y= compomente rectangular en y del vector.
r = HIP = magnitud del vector.
α = ángulo al que se está refiriendo.

Ya sabiendo tooooodo esto, se pueden hallar los componentes del vector.

Encontrar los componentes de un vector en un plano x, y.

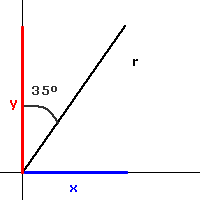
Se tiene un vector B de 45N con α = 35º con respecto al eje y positivo. sus componentes rectangulares se encuentran de la siguiente manera: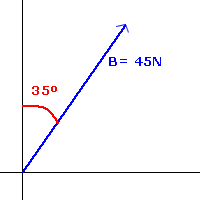

	1.- Se traza el vector con la información que nos dan. La longitud de la flecha debe ser de 45 unidades. La inclinación debe de ser de 35º hacia la derecha del eje positivo de las y. Si α hubiera sido -35º entonces la flehca se trazaría con 35º de inclinación hacia la izquierda del eje positivo de las y. Ahora respira ondo qué lo que sigue es lo único que vale la pena en este mar de paja.
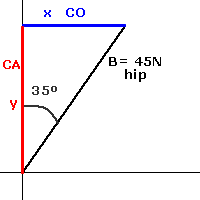	2.- Se trazan las componentes rectangulares. Y se usan funciones trigonométricas para encontrar sus valores. Como y es el cateto adyacente al ángulo, se puede calcular su valor despejando y de la función coseno. 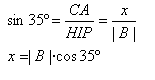Como x es el cateto opuesto (en este caso) al ángulo, se puede calcular su valor despejando x de la función seno. la componente x es, en este caso, el cateto opuesto a α, entonces x = 45*(Cos α)=36.861 N. la componente y es, en este caso, el cateto adyacente a α, entonces y = 45*(Sin α)=25.810 N.
	El mismo proceso funciona en reversa y se le llama composición de vectores. y consiste en hallar la resultante r de varios vectores. se sustituyen los valores de las componentes en el teorema de pitágoras y queda algo así: 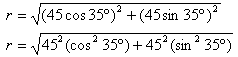se saca el 45 hay una identidad trigonométrica que dice que coseno cuadrado de un un ángulo + seno cuadrado del mismo ángulo es = 1, entonces: r = √(45 ^2) = 45